How Biased Are Demand Estimates?

Table of Contents

• Overview
• The State of Demand Invalidity
• Hypothetical Bias is Upward, Not Downward
• How Much Should We Calibrate Demand Estimates?
• Some Simple, Evidence-Based Solutions for the Bias Problem
• Taking Economic Advice with a Pinch of Salt
• Take-Home Points

Overview

We’ve written extensively about the challenges of successfully executing demand studies in life science in other posts, but today we want to tackle what might be the biggest issue with these studies.  Why are the estimates so often wildly different than what ends up happening in the market?   This post explains the nature of bias that creeps into our estimates of customer demand for hypothetical new medicines.  We explain the economic origins of the study of bias, as well as the practice of calibration.  Our main focus will be to share the best and most contemporary evidence about the size and direction of estimation bias, and to offer an up-to-date view on how we might approach the practice of calibration based on evidence rather than on arbitrary business rules.  We also offer some first-order suggestions for how to minimize bias in your own study designs. 

Readers will come away with evidence-based answers to the following questions.

• How big is estimation bias, really?
• Should we calibrate, and if so, how much?
• What else can we do to minimize estimation bias?

The State of Demand Invalidity

Before we talk about the direction and magnitude of estimation bias, it may be helpful to anchor ourselves to some basic ideas.  Demand studies are, first and foremost, estimates of market share.  In principle, a demand study might deliberately attempt to reflect any point on the uptake or diffusion cycle of the product (see the orange circle in Figure 1 below for an example).  However, in most cases, we are explicitly trying to estimate peak share – that is, the conceptual high point of market penetration that a product will achieve during the arc of its commercial life.  Peak share is an elusive concept in its own right because market penetration can be hard to measure.  Nevertheless, demand estimates are normally said to be “invalid” to the extent that they depart from actual or observed peak market share.  As you can see from the figure, invalidity can live on either side of the true peak share, in that a demand study may over-estimate or under-estimate the true future state of affairs. 

Figure 1.  How Demand Estimates Relate to Actual Drug Adoption “In the Wild” 

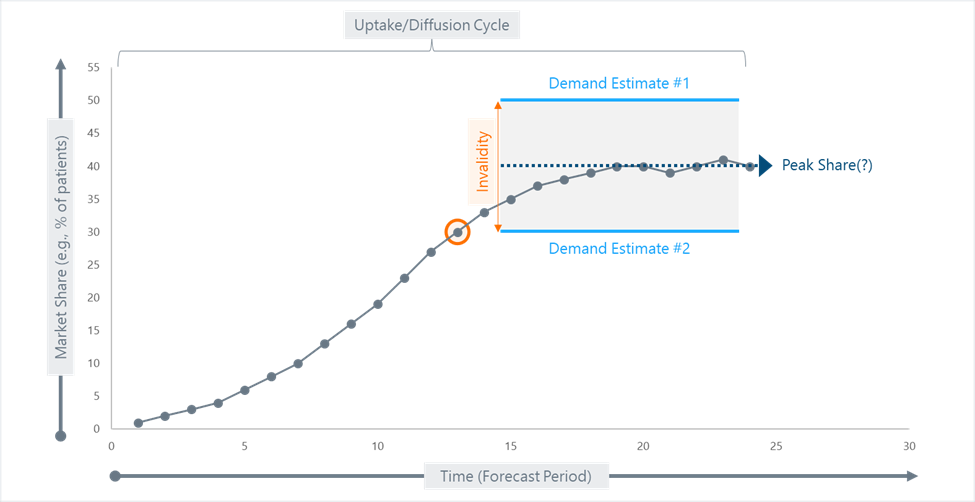
While Figure 1 is helpful for giving us a mental model of what we mean when we talk about demand studies in the context of a forecast, it is misleading in one way.  The figure shows two equally sized invalidity vectors – one for Demand Estimate #1, which is too high and one for Demand Estimate #2, which is too low.  This implies that demand studies may be equally likely to be wrong in both directions, as is asserted by some authors.¹  However, academic researchers who study these questions for a living have demonstrated pretty conclusively that the general trend in estimation bias is nearly always upward.

Hypothetical Bias is Upward, not Downward

In the world of economics, the bias that emerges when we ask customers to think about their future behavior is called hypothetical bias.  It’s called that because the scenarios they test in research are normally hypothetical rather than real.  That distinction should matter to us, and it certainly does to economists, who worry that the absence of true economic costs and direct experience rob these exercises of psychological realism, and thus distort the truth of what people will do.  Our demand studies are normally very similar to these experiments, in that we have customers predict their own behavior with respect to some hypothetical product in a hypothetical future.  Importantly, most economists are focused on the price that customers were willing to pay for a hypothetical good (which gives us the term, willingness-to-pay), which is not what we mean by customer demand in Life Science. 

The uniform view, based on experimental evidence, was that hypothetical bias was nearly always in the upward direction.  In other words, what customers said they would be willing to pay turned out to be much higher than what they would pay in real life.  Over time, many studies have been conducted to figure out things like:

• How large is the hypothetical bias?
• Does the bias differ for different types of goods?
• What techniques mitigate it? 

Until recently, the hypothetical bias effect was thought to be enormous.  But because of the proliferation of studies comparing hypothetical willingness-to-pay (WTP) against real willingness-to-pay, researchers are now able to use meta-analysis to understand the nature of the hypothetical bias phenomenon with far greater precision than could be achieved based on a small handful of experiments.  The two most relevant meta-analyses that address the question are summarized in Table 1 below.  The 2005 analysis was focused mostly on public goods (as in, how much would people be willing to pay to ensure things like clean water and a stable environment), whereas the 2020 analysis focused deliberately on WTP for private goods (as in, things that you would buy, use, or consume personally).  Both analyses looked at the ratio of hypothetical willingness to pay compared with actual/real/observed willingness to pay derived from experiments that measured both endpoints. 

Table 1.  How Big is the “Hypothetical Bias” 

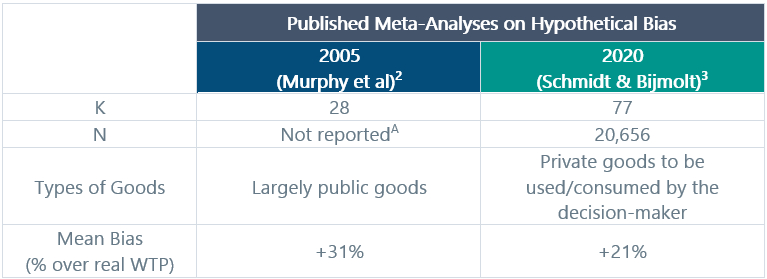
^A This meta-analysis is a reevaluation of an earlier meta-analysis published in 2001 by John List and Craig Gallet.  Neither the original 2001 paper, nor the 2005 re-analysis reports the sample sizes used in the original studies. 

These data represent the closest thing that I can find in academic literature to a true estimate of bias in hypothetical exercises like the ones we use in demand estimation.  We can draw two conclusions:

1. The bias is very clearly in the upward direction.
2. The magnitude of the bias is really not that big, and certainly would not justify the reflexive tendency to just “cut it in half” that we sometimes hear about in conversations about calibration.

It is worth noting one key distinction regarding the Schmidt et al (2020) meta-analysis.  This is the first and only such assessment to look exclusively at bias relating to what economists call private goods.  This means that the participants are making estimates about things that they will actually purchase, use, or consume directly.  While neither public nor private goods as studied by economists are a perfect analog for the kinds of decisions that we study in life science demand studies, I submit that private goods probably represent a better point of comparison with the use of medicines.  In most cases, the participants in the private goods studies are reasonably familiar with the nature of the products they are speculating about.  Similarly, physicians (and even patients) will have a fairly intimate understanding of the basic nature of a new medicine even in situations where the product represents a new category or MOA.  My point is that the 2020 meta-analysis is probably our best guide for estimating the normal scope of bias that we could expect in our own demand studies.

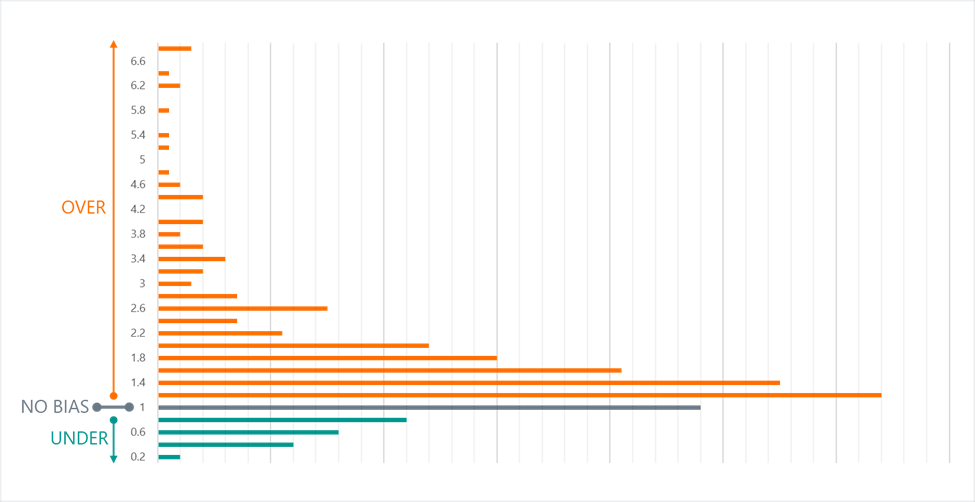
Overall, Table 1 should offer some reassurance to marketers and insights professionals.  At least in the world of pricing, the hypothetical bias is not that large.  However, before you grab a calculator to determine your calibration ratio, it is worth noting that each of these meta-analyses also showed that the distribution of bias across the included studies was very positively skewed.  In Figure 2 below, we present data from a 2017 meta-analysis that reported the actual frequency distributions of the ratio between estimated and real willingness-to-pay.⁴  We present their data with additional clarifying labels. The main learnings here are:

• We can see that most estimates fall between a ration of 1.0 (no bias) to 2.0, as we would expect based on the previously cited meta-analyses. 
• But we can see the long tail of upward bias that can stretch all the way up to 7 (i.e., hypothetical estimates being 7x the real-world willingness-to-pay).

The skew observed here is also referenced explicitly in the 2005 meta-analysis, though the data are presented in a less dramatic format.  The nature of the skew in Figure 2 should make all of us pause and think twice when we are tempted to simply apply a calibration factor to our demand studies.

Figure 2.  Upward Skew in Studies of Hypothetical Bias

As a closing comment on this topic, in more than 20 years of doing demand studies and then cross validating those estimates against estimates of real peak share, I can qualitatively affirm that using conventional demand techniques, the prevailing direction of “wrongness” is on the high side.  In fact, I can only call to mind a few occasions where a demand study turned out to be too low when using, say, an allocation task.  Of course, my subjective experience is no substitute for the academic evidence presented here. 

How Much Should We Calibrate Demand Estimates? 

Many of us in the world of customer insights will be familiar with the practice of calibration, which involves using a numeric business rule to adjust or right-size estimates of customer demand.  The most common rule-of-thumb for calibration that I have heard of are:

• Cut the number by 50%.
• Cut the number by 33%.

I doubt very much that these conventions arose from nothing more than someone’s arbitrary assessment that a study output “just felt too high.”  While I cannot be 100% certain about the origins of the practice, my incursions into the literature suggest that it too stems from economics.  Beginning in the 1960s, as researchers began to study the hypothetical bias problem, the term calibration factor appears more or less simultaneously.⁵  The calibration factor is the coefficient that you would multiply against the hypothetical willingness-to-pay estimate in order to (ostensibly) make it line up with real willingness-to-pay.  If you examine the previously-mentioned meta-analyses from 2005 and 2017, you will see that the calibration factors reported for individual studies are all over the place.  This makes sense given the skewed distribution of estimate bias that we saw a moment ago.  And if you just glance at Table 1, you can also see that many, many experiments comparing hypothetical to real willingness-to-pay yield ratios in the range of 2.0, which would correspond exactly with the “cut by 50%” rule that we often see in practice.  At the same time, many studies also fall somewhere in the neighborhood of 1.4 to 1.6, which would correspond approximately to the “cut by 33% rule.”  If you were conducting a qualitative literature review, you might naturally come away with these as basic recommendations. 

However, it turns out that the “cut by 50%” guidance was more recommended in a much more formal setting.  Specifically, a 2001 report to the National Oceanographic & Atmospheric Administration (yes, you read that correctly) by a group of economists proffered a qualitative recommendation that valuations made from hypothetical research on public goods should be cut in half by default.⁶ The report is interesting and well-written, and carries the imprimatur of some very impressive names from the world of economics.  Frankly, I suspect that the practice of cutting demand numbers in half pre-dated this report, but I also suspect that this affirmed and codified the practice. 

Still, I hope it’s obvious that the contemporary assessment of estimation bias suggests that this kind of “haircut” would create a serious over-correction problem.  Table 2 below translates the original meta-analytic bias estimates from Table 1 into their corresponding calibration factors.  Compare these to the factors of 0.5 and 0.66 implied by our two “rule of thumb” approaches.

Table 2.  Evidence-Based Calibration 

To be fair, the papers cited in the NOAA panel report were conducted in the 1970s through the 1990s, and many of those experiments demonstrated very high bias ratios.⁷ Additionally, the kind of rigorous meta-analytic synthesis conducted by Schmidt et al was still a very new idea in 2001. As such, their recommendation makes sense in context.  I also think it makes sense to update our practices based on the best contemporary evidence that we have. 

So, does it make sense to calibrate your demand estimates?  As a practitioner, I have shied away from making calibration recommendations in the past for two good reasons.  First because I think that the degree of bias in our measures can be controlled with better question-architecture rather than calibration.  And second because of the kind of data we have seen here.  The bias effect is just not big enough to justify this kind of chopping.  Nevertheless, I suspect the practice will continue if only due to industry culture and the effects of habit.  With that in mind, my suggestion to practitioners is to consider using more modest calibration coefficients, such as those that would be suggested by the two meta-analyses cited above.  This will make you less likely to over-correct, particularly if you are also using evidence-based techniques for structuring and contextualizing your demand estimate.   For example, if you did a demand study and captured a weighted peak share estimate of 20%, you would calibrate this to 15.4% rather than to 10% (a 50% haircut) or to 13.2% (which is a 33% cut). 

Some Simple, Evidence-Based Solutions for the Bias Problem

Hopefully, you are at least somewhat persuaded that the upward bias in demand estimation is real and, in most cases, not nearly as bad as our habitual calibration practices would suggest.  A logical follow-up question is, can we do anything else to reduce the bias?  Of course, the answer is yes and naturally, there can be a range of options.  We will offer a more comprehensive view of specific techniques in a separate post, but for now we will summarize some solid, easy-to-use techniques that have been well-vetted by academic researchers.   

Suggestion 1 – Use Script-based Priming (aka “Cheap Talk” method):

Beginning with a 1999 study, some researchers began to investigate the use of cognitive manipulations within their hypothetical pricing and choice task structure.  The “Cheap Talk” method involves the use of a simple script that is inserted prior to the actual hypothetical estimation task, where the script explains the phenomenon of overstatement bias and implores the participant to account for this in their answers.⁸  This is a nice example of a “cognitive speed bump” that can be used to improve the thinking (and thus the quality) of participants’ estimates, and which can be easily adapted to life science.  In your own demand studies, you might say something like the script below.

Doctor, the estimates you provide are very important to [business or insights goal].  Historically, participants in this kind of research tend to overstate their use of new products to a significant extent.  This overstatement limits the value of the findings and can have serious implications for product supply and access.  In the following exercises, please do your best to provide the most realistic estimates you can. 

In the above-referenced 2005 meta-analysis, the researchers found that this kind of simple script-based manipulation reduced the scope of upward bias in WTP exercises by 33.1%.  That’s a pretty strong outcome for such an easy manipulation.

Suggestion 2 – Use Certainty Correction (with caution): 

Another simple bolt-on to your demand exercises that is already in common use is certainty correction.  The idea is that you ask participants to rate their own certainty about their estimates on a scale (e.g., 1 to 7, or 1 to 10).  From there, you either up-weight the more certain participants or you only use the estimates from participants who are above a certain certainty threshold.  Practically everybody already knows to do something like this, and in our own professional lives, we have used this type of certainly adjustment in a wide range of demand settings.  The big challenge here, which the authors of the 2005 meta-analysis are quick to point out, is that nobody has figured out exactly where the cutoff should be.  In their analysis, they simply took the certainty-corrected figures provided by the individual study authors at face value.  The results are shown in Table 3 below. 

Table 3.  The Effects of Certainty Correction on Estimation Bias

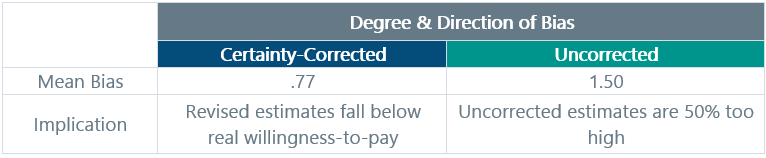
At first pass, you might simply dismiss certainty-correction because it seems to over-correct, landing us in a place where we are now underestimating demand.  But consider that many of the included studies used fairly draconian rules for certainty correction (e.g., only those participants rating 8 or higher on a 1-to-10 scale are counted).  So, a simple solution is to use certainty correction a bit more “gently.”  For example, you might choose rules like:

• Count anyone who rates 4 or higher on a 7-point scale
• Count anyone who rates 6 or higher on a 10-point scale

Obviously, these are judgment calls, but that doesn’t mean the technique doesn’t work. 

Additionally, there is one more evidence-based point to make here before we move on, and this one may be surprising.

Suggestion 3 – Do Not Expect Choice-Based Exercises to Solve the Estimation Bias Problem:

This might seem like an admonition rather than a recommendation, but hear us out for a moment.  The 2020 meta-analysis summarized in Table 1, which represents the largest and most applicable synthesis of the estimation bias phenomenon available to-date, also did a specific sub-analysis comparing the degree of inflationary bias associated with direct measurement exercises compared with indirect/choice-based exercises.  They did this because, for years, choice-based exercises have been put forward as uniformly better than standard hypothetical estimation methods that ask customers to estimate their willingness-to-pay with a direct question.  The meta-analysis showed that choice-based methods systematically led to larger bias – specifically an increase of +10% in total bias.  In other words, conjoint and DCM-style procedures actually increased the degree of inflationary bias in hypothetical vs. real-world comparisons.  We will have more to say about choice-based experiments in another post, but for the moment, the evidence is clear:  You will get less upward estimation bias if you simply ask the participants to directly state their estimates rather than deriving them from a choice model. 

Taken together, these simple methods are likely to go a long way toward reducing (and probably nearly eliminating) the inflationary tendency attached to demand research and improve the quality and predictive accuracy of your peak share estimates.  Readers interested in more techniques for improving demand data quality are encouraged to check out our post entitled, “Can People Accurately Predict Their Own Behavior”. 

Taking Economic Advice with a Pinch of Salt

We want to close this topic by pointing out something that might be obvious already:  The economic concepts and the extensive data presented here are clearly relevant and informative for our demand work.  But there are some conceptual disconnects that should make us cautious about assimilating these ideas without adding a pinch of salt.  My concerns are as follows.

• Willingness-to-Pay is Not the Same Thing as Demand for a Medicine:  When economists explore the question of what consumers will pay for a public good or a private good (one they will consume or use themselves), they are literally talking about the dollar amount they will pay.  But neither physicians nor patients (mostly) pay directly for their medicines.  Further, within a demand study, what we are typically asking physicians and patients to anchor to is not price at all, but rather what they will do.  Demand is about how much you will use, NOT how much you will pay. 
• Willingness to Pay is Not Even the Same Thing as Preference:  Similarly, from a psychological perspective, willingness-to-pay is also not the same thing as preference.  Asking me what I would pay for a specific good or service is one thing.  Asking me what I would prefer from among a set of options is completely different. 

Yet many economists use these ideas more or less interchangeably.  That makes more sense in the world of consumer goods where each person can make unimpeded decisions about what he or she wants to buy.  But medicine is different.  The exercises simply have different properties, including multiple influential stakeholders, proxy decision-making and much more serious consequences, such as toxic side effects.  My point is that we should not assume that the research from economics would apply perfectly to the estimation of product demand by treaters or by patients.  Instead, I think we should treat this science as a rough starting point for our own empirical investigations.

Take-Home Points

• Most of the evidence we have about bias in estimations about hypothetic use of goods comes to us from studies in economics that focus on willingness-to-pay. 
• On balance, such estimates will nearly always be inflationary rather than deflationary relative to actual behavior or actual decision-making in the real world.  This is why we speak of an inflationary bias in life science demand studies. 
• The best and most contemporary estimates we have from empirical research indicate that the degree of inflationary bias is 21% on average.  However, the distribution of bias is sharply skewed in the upward direction.  Studies that reveal inflationary ratios of 2 or 3 (i.e., 200% or 300% above observed willingness-to-pay) are not uncommon. 
• Calibration should be approached with caution because of the tendency for hypothetical estimations to be heavily skewed.  Based on the most recent and robust evidence, a calibration coefficient in the range of .77 to .83 would be more defensible. 
• But simple methodological “fixes” for upward estimation bias are also available and easily built into any primary demand study. 

To learn more, contact us at info@euplexus.com.

About euPlexus  

We are a team of life science insights veterans dedicated to amplifying life science marketing through evidence-based tools.  One of our core values is to bring integrated, up-to-date perspectives on marketing-relevant science to our clients and the broader industry.